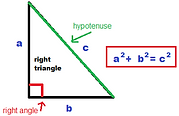
My name is Stacey and I love to learn. I think that teaching people how to think critically makes the world a better place. As someone on the Autism spectrum, I sometimes learn differently than other people. I tend to be drawn to organized lists and graphs and repeat things I find interesting to myself over and over. I like to analyze how and why things work the way they do. Math is something I excel at sometimes and struggle with other times, depending on the topics. There have been times I explained things to the teacher and times I really hated math. In Grade Nine, I had a teacher who was demonstrating the pythagorean theorem and applying it to a problem where she was trying to find the height of a wall based on the height of a ladder leaning on that wall and the distance between the base of the wall and the base of the ladder. I had to explain to her that the ladder, not the wall, was the hypotenuse. In Grade Eleven I did advanced math and did alright but went back to academic math the next year in order to get a better grade. In university I did the math that was supposedly the easiest but I think it was just different as opposed to easier than the other courses. I learned about sets, logic, counting systems, and relearned finding area and volume. I did not do as well as I would have liked, as I was still adjusting to university and struggling with other courses like French. Professionally, as someone who wants to help create workable and inclusive curriculum, I believe that children should be taught multiple approaches to each problem and be encouraged to come up with their own, this way they can solve problems in the way that is most efficient for them. I also believe emphasis should not be on getting the right answer, but on the process involved. Students should not be afraid of making mistakes while they are learning to understand how the math works. That is the core of my math philosophy: understanding how math works. I believe it is not enough to teach a student a formula for solving an equation. They will not know how to identify when and how to use it or notice when an answer does not seem right.  Nor will they be able to draw on prior knowledge when learning how to solve more complex problems. Understanding what is actually happening when solving a problem is crucial to being able to apply the understanding to other problems and thus building on skills. When my Grade Nine math teacher tried to solve the problem involving the ladder and the wall, she was using procedural knowledge, remembering that the usual way to use pythagorean theorem was to square two sides, add them together, and find the square root. However, she was not understanding that this particular problem involved first determining which side was which and applying the thereom in reverse, using the square of the hypotenuse to determine the square of another side. The problem required more than procedural knowledge, it required a through understanding of how pythagorean theorem works and how to apply it to new situations.